Gabriella Pinter from UWM’s mathematics department joined us for our November 13th session. Gabriella runs a Math Circles program at UWM for middle and high school students (http://uwm.edu/news/math-circle-taps-kids-creativity-in-problem-solving/) as well as a second program for area K12 teachers. She gave our group a minds-on experience of the process.
The Math Circles approach is to explore a problem (which may or may not have a known answer) to see where the ideas lead, test whether a solution can be proven, and see what new questions those discoveries raise. As with meaningful discourse, it allows students to collaboratively build their understanding of the problem at hand, drives students to think carefully about what they do and do not know, and, as the problem is discussed, makes that thinking visible not only to the teacher but the other students in the room.
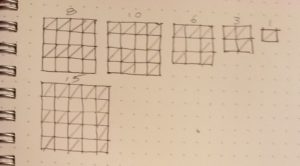 For our exercise, Gabriella asked us to play a game within a 4 x 4 grid. The rules of the game are pretty simple: You may put a single diagonal line running from corner to corner in any cell of the grid, so long as neither end point of that diagonal touches an end point of a diagonal in any adjoining cell. Go.
For our exercise, Gabriella asked us to play a game within a 4 x 4 grid. The rules of the game are pretty simple: You may put a single diagonal line running from corner to corner in any cell of the grid, so long as neither end point of that diagonal touches an end point of a diagonal in any adjoining cell. Go.
It doesn’t take long for the question to surface– how many diagonals can one place in the grid? The group’s consensus, 10.
How about a 3 x 3 grid? 6.
2 x 2 Grid? 3.
1 x 1 grid? Well yeah, 1.
5 x 5? 15…. Are you sure?
Well it looks like we have a pattern of triangular numbers…
| Grid Size | 0 | 1 | 2 | 3 | 4 | 5 |
| Diagonals | 0 | 1 | 3 | 6 | 10 | 15 |
Take the last number of diagonals, add to it the next grid size, get the next number of diagonals:
0 + 1 = 1
1 + 2 = 3
3 + 3 = 6
6 + 4 = 10
10 + 5 = 15
So we have a pattern and that looks like a pretty good rule. Is it a proof? er…. maybe?
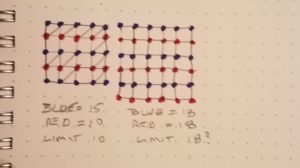 What else have we seen? Well, each diagonal we place uses up two potential end points on the grid. On a 4 x 4 grid, if we mark these potential end points as alternating rows of blue and red dots, starting with blue, we will have 3 rows of 5 blue dots and 2 rows of 5 red dots. With that pattern, every diagonal must touch a red dot. There are only 10 red dots, seems like a pretty good proof that 10 is the limit for a 4 x 4 grid.
What else have we seen? Well, each diagonal we place uses up two potential end points on the grid. On a 4 x 4 grid, if we mark these potential end points as alternating rows of blue and red dots, starting with blue, we will have 3 rows of 5 blue dots and 2 rows of 5 red dots. With that pattern, every diagonal must touch a red dot. There are only 10 red dots, seems like a pretty good proof that 10 is the limit for a 4 x 4 grid.
Ok, what about a 5 x 5 grid? Now, for both blue and red dots, we have 3 rows of 6, and therefore an upper limit of 18 diagonals. So what is possible 15, which we found, 18 which is clearly the upper limit, or something in between? Please tell us how you found 16.
……………………..
The wonderful thing to see in this process was how Gabriella slowly released a little bit more of the problem to explore just as the group thought it had arrived at an answer. It was a very effective way of keeping engagement and interest high by continually adjusting the bounds of the problem to a point just beyond what we knew.
Gabriella pointed us to www.mathpickle.com which has a wonderful collection of problems to explore for any grade level.
Up next for the group, math journals.
The Middle School Math Workgroup is a collaborative effort with Milwaukee Succeeds to explore practices which drive student performance and share ideas and experiences about bringing those practices into the classroom.

