Our workshop at this year’s System Thinking Institute focused on how to increase the adoption of meaningful discourse within math lessons. As we noted in our last post, recognizing that a practice is effective is not enough. If we want to see widespread and sustainable adoption, the practice must be part of a larger solution that solves a real problem for teachers.
To understand how we might do that, we teamed up with Danielle Robinson, the Math Interventionist from Brown Street Academy. Danielle lead the group through an exploration of their hopes and fears around introducing meaningful discourse into the classroom. In the afternoon, we used that to guide a discussion of the factors that drive the decisions teachers make as they plan their lessons.
After the first day’s session ended, we sifted through everything we heard to construct a profile, written from a teacher’s perspective, that summarizes how they think about meaningful discourse, and what that means for their planning. Day 2 began with a discussion of this profile. You can view the complete profile here.
Moving Towards a Solution
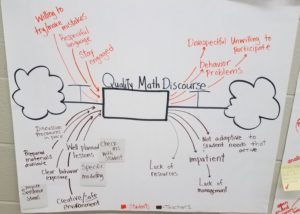With our profile in hand, Danielle led us through a look at factors that drive or hinder quality math discourse in the classroom. That set the stage for us to identify four key problems teachers face as they seek to introduce discourse or Number Talks in their classrooms:
- Number talks are new to me and I’m not comfortable trying them out on my students
- I don’t know how I will assess how my students are doing when I use a number talk as part of a lesson
- I worry about being to reach all students in my class
- I don’t have the resources (tools, time, support) to do number talks well/get good at doing so quickly
Using a version of the Lean Startup Canvas we’ve adapted for looking at programs within schools, we had the group sketch out what a solution might look like. You can see the canvas we put together here.
The approach we arrived at equips classroom teachers with tools, resources, and support to drive quality discourse in a way that allows it to take root, and commit to seeing that it does. Here’s what that looks like:
Tools
- Set of common terms/behaviours to be used by teachers working on meaningful discourse
- List of sentence starters teachers can use to guide students
- Quick Checklist for Number Talk lessons, that identifies strategies students might use in the exercise as well common misunderstandings. The checklist should provide an easy way for the teacher to make note of the strategies and/or misunderstandings of individual students. It should also indicate how the lesson relates to standards (MTAP?)
- Best practice anchor charts for Number Talks
- Use Reflection Journals to have students reflect on their own learning/approaches
- List of ideas for math challenges teachers can use to check understanding
Resources
- In-building math specialist who is available for in-classroom modeling of meaningful discourse and ongoing support/mentoring as teachers develop their skills in leading math discourse.
- In-building cohort of teachers working to integrate meaningful discourse into their lessons, and support each other in doing so.
- Cross school network of teachers working to expand the use meaningful discourse in their schools.
- Peer-based professional development that respects the voice of teachers.
- Schedule changes that would allow teachers to observe/provide feedback to each other.
Support
- Overt support from building leadership for teachers who elect to integrate meaningful discourse into their math lessons.
- Permission from district administration for teachers to deviate from the pacing guide based on their students’ needs.
Next Steps
We treat everything on the canvas as a hypothesis to be tested. The key assumption to validate first is that the problems we identified are issues for teachers beyond those in our session. There is no point investing time and money in a solution if we aren’t focused on the right problem.
We had a number of Danielle’s colleagues from Brown Street in our session, but as a first step, we’ll look to review the list of problems we came up with to confirm that these are important to a wider group of teachers at her school. Assuming these teachers see the same set of issues, the group identified a series of actions we could take both before the end of this school year as well as over the summer to lay the groundwork for a strong start in the fall.
- Converting a CAB to a number talk
- (continue to) Provide intervention to students that need extra instruction
- Practice Number Talk procedures
- Establish a common language for Number Talks (“turn and talk” vs “shoulder partners”)
- Create prototypes for tools– sentence stems, anchor charts, checklist
We’ll review were we landed at the next meeting of our Middle School Math workgroup. We don’t want to lose momentum coming out of the workshop, so we’ll continue to work with Milwaukee Succeeds and Danielle and her colleagues from Brown Street Academy to move this forward.
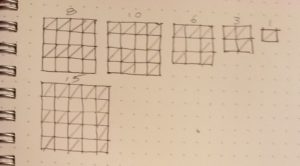For our exercise, Gabriella asked us to play a game within a 4 x 4 grid. The rules of the game are pretty simple: You may put a single diagonal line running from corner to corner in any cell of the grid, so long as neither end point of that diagonal touches an end point of a diagonal in any adjoining cell. Go.
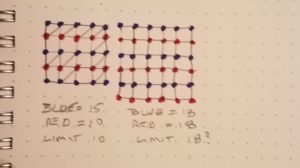What else have we seen? Well, each diagonal we place uses up two potential end points on the grid. On a 4 x 4 grid, if we mark these potential end points as alternating rows of blue and red dots, starting with blue, we will have 3 rows of 5 blue dots and 2 rows of 5 red dots. With that pattern, every diagonal must touch a red dot. There are only 10 red dots, seems like a pretty good proof that 10 is the limit for a 4 x 4 grid.