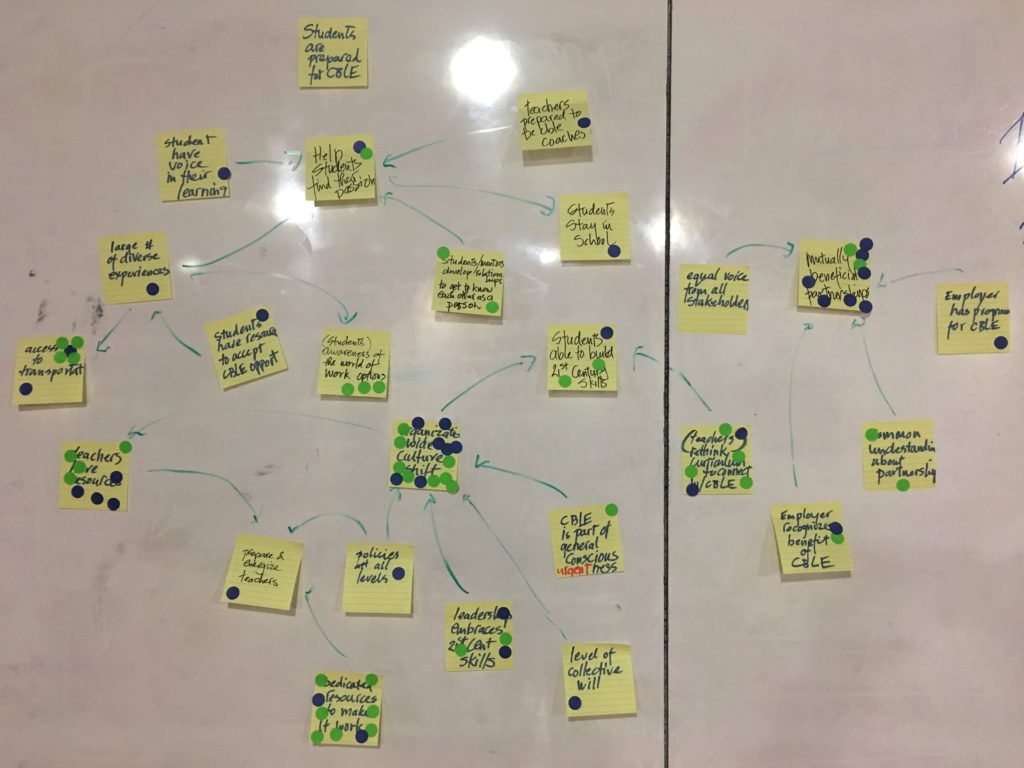
We put together our November session with help from Susan Koen and Stacey Duchrow from Milwaukee 7’s Regional Talent Partnership. In their work to help develop the talent pipeline for industry in southeastern Wisconsin, they see a number of systemic issues that get in the way of effective career based learning experiences for students. We set up the session with the aim of mapping out factors which contribute to successful CBLE’s and identifying the key places where collaborative efforts might make a difference.
For this session, we split the attendees across 5 tables, where each participant shared their thoughts on key goals, and came together as a team to share those the felt were most important with the entire group. These included:
- Help students find their passion
- Students/Mentors develop relationships that allow them to know each other as a person
- Students Stay in School
- Students are able to build 21st Century skills
- Teachers are prepared and energized
We followed this with a second round of where participants shared their thoughts on key factors which help reach those goals or stand in the way. Again, each table came to a consensus on on the key factors to share out with the larger group. These include:
- Students are prepared for CBLEs
- Students have a voice in their learning
- Students have access to a number of diverse experiences
- Students have the resources (transportation, etc,) to accept CBLE opportuntities
- An organization wide culture within schools supports CBLEs (as opposed to a focus on college preparedness)
- Teachers have the resources they need to deliver on their end of CBLEs
- Policies (state & district) support CBLEs
- Leadership embraces 21st Century skills
- The level of collective will (in support of CBLEs)
- CBLE is part of general conciousness
- Employers recognize the benefit of CBLEs
- Teachers’s ability to connect curriculum to CBLEs
- Schools/industry have a common understanding of what a partnership requires
- All stakeholders have an equal voice
- Employers have program in place to support CBLE
- Teachers are prepared to be coaches
- Schools/partners have dedicated resources to make CBLEs work
As we talked through each of these factors in turn, we built up a map that gave us a first draft how these factors influence each other, and thereby, the goals we have for CBLEs. We ended the session by having the participants identify, by placing dot stickers on our map, the factors they felt were most important. The key items for the group as a whole:
- An organization wide culture within schools supports CBLEs (as opposed to a focus on college preparedness)
- Schools/partners have dedicated resources to make CBLEs work
- Schools/industry have a common understanding of what a partnership requires
Next Steps
We’ll be working with Milwaukee 7 to pull together follow on sessions to drill into each of the top three factors and from that, identify where collaborative efforts could make a difference. Interested in participating in one of these sessions? Let us know:
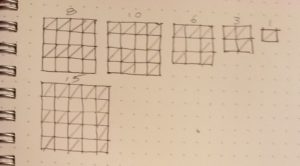For our exercise, Gabriella asked us to play a game within a 4 x 4 grid. The rules of the game are pretty simple: You may put a single diagonal line running from corner to corner in any cell of the grid, so long as neither end point of that diagonal touches an end point of a diagonal in any adjoining cell. Go.
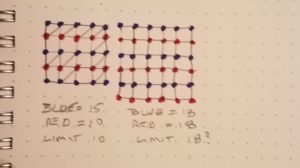What else have we seen? Well, each diagonal we place uses up two potential end points on the grid. On a 4 x 4 grid, if we mark these potential end points as alternating rows of blue and red dots, starting with blue, we will have 3 rows of 5 blue dots and 2 rows of 5 red dots. With that pattern, every diagonal must touch a red dot. There are only 10 red dots, seems like a pretty good proof that 10 is the limit for a 4 x 4 grid.